Ce post est fondé sur les résultats montrés dans le chapitre 5 du livre. Tous les commentaires sont les bienvenus.
“Eh bien, dans NOTRE pays,” dit Alice, toujours un peu essoufflée, “vous arriveriez généralement quelque part ailleurs — si vous couriez très vite pendant longtemps, comme nous venons de le faire.” “Un genre de pays lent!” dit la Reine. “Maintenant, ICI, vous voyez, il VOUS faut courir autant que vous le pouvez, pour rester au même endroit. Si vous voulez aller quelque part ailleurs, vous devez courir au moins deux fois plus vite que ça!”} (https://victorianweb.org/authors/carroll/zrd/2.htm)
Au début des années 1930, Kalecki écrit une série d’articles et publie son fameux Essay on the Business Cycle Theory (1933). Dans ces travaux, il développe la vision d’un monde asymétrique où les capitalistes sont « maîtres de leur destin » à la différence des salariés. En tant que classe, les capitalistes gagnent autant qu’ils dépensent. En tant qu’individu, cependant, ces derniers n’ont aucun contrôle sur les décisions prises par les autres et finalement sur ce qui leur arrive individuellement.
Une version mathématique de cet Essay est présentée lors du troisième congrès européen de la Société d’économétrie à Leyde en 1933. Dans sa communication, Kalecki expose ses idées sur la base d’un outil mathématique introduit par Jan Tinbergen (1931). Le modèle comprend quatre équations. En le résolvant analytiquement, Kalecki montre que, avec une estimation approximative des paramètres (les paramètres 
et 
étant les coefficients de la fonction d’investissement et représentant le temps nécessaire à la construction des biens d’investissement), son modèle conduit à l’existence d’oscillations auto-entretenues, d’une durée moyenne de dix ans.
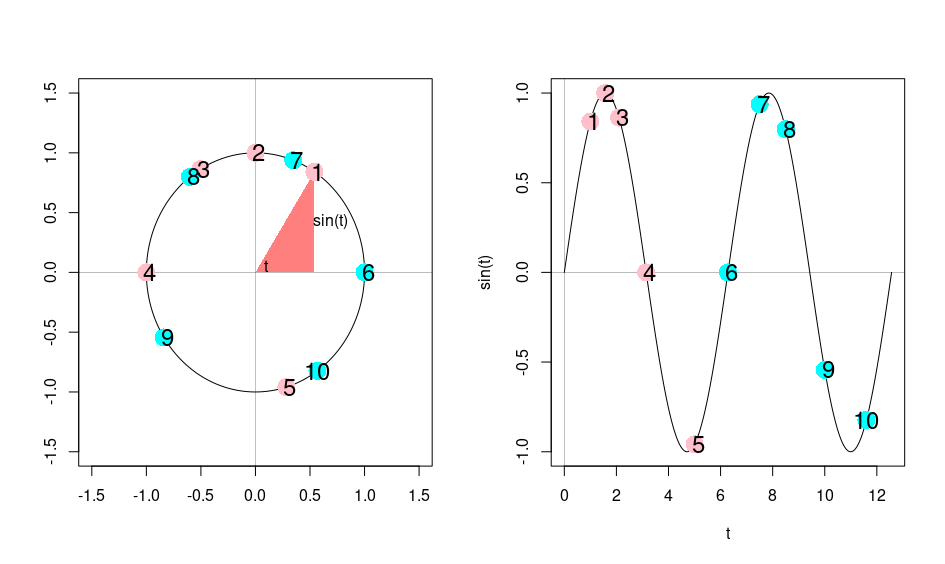
La métaphore introduite par Lewis Carroll dans son roman Alice de l’autre côté du miroir colle bien au message de Kalecki. Comme la « Reine de coeur » qui est surprise de ne pas bouger d’un pouce alors qu’elle coure, les capitalistes pris dans la course aux profits n’ont aucune prise sur l’économie. Le cycle auto-entretenu représenté par une fonction sinusoïdale est l’illustration du cercle infernal dans lequel sont pris les capitalistes, chacune des coordonnées du cercle correspondant à un moment du cycle économique. Comme on peut le voir, l’économie revient invariablement à son point d’origine, les capacités productives et le revenu national n’ayant pas varié. Cela démontre pour Kalecki que la course effrénée aux profits laisse l’économie inchangée et dans un état de stagnation.
Le cercle doit être lu dans le sens anti-horaire, à droite nous représentons la fonction sinus en fonction du temps ‘t’, où ‘t’ peut également être vu comme l’angle dans le cercle entre l’axe horizontal et une ligne tirée de l’origine à un point sur le cercle.
Ce modèle met également en évidence l’indépendance entre les mouvements cycliques et le pouvoir que les capitaliste exercent au sein de leur propre organisation ou de ce que Marx appelait la « sphère de production » (extraction de la plus-value). Dans la pensée de Kalecki, les profits proviennent de la « sphère de circulation » (réalisation de la plus-value) où les biens sont vendus et les profits sont réalisés. Pour cette raison, une hausse de la marge bénéficiaire (ou « markup ») que les capitalistes pourraient gagner à la suite d’une lutte avec les salariés ne peut leur bénéficier en tant que classe comme c’est le cas chez Marx. Tant que les capitalistes gagnent autant qu’ils dépensent, ce changement dans la répartition du revenu s’accompagnera d’ajustements de l’emploi et de la production qui laissera le niveau des profits inchangé: les capitalistes gagneront simplement une part plus grande d’un revenu national plus faible. Politiquement, en revanche, la lutte des classes peut avoir un rôle considérable dans la mesure où elle peut orienter la politique économique, diplomatique et militaire. Ce n’est que de cette manière indirecte que les capitalistes ont en définitive prise sur l’économie.
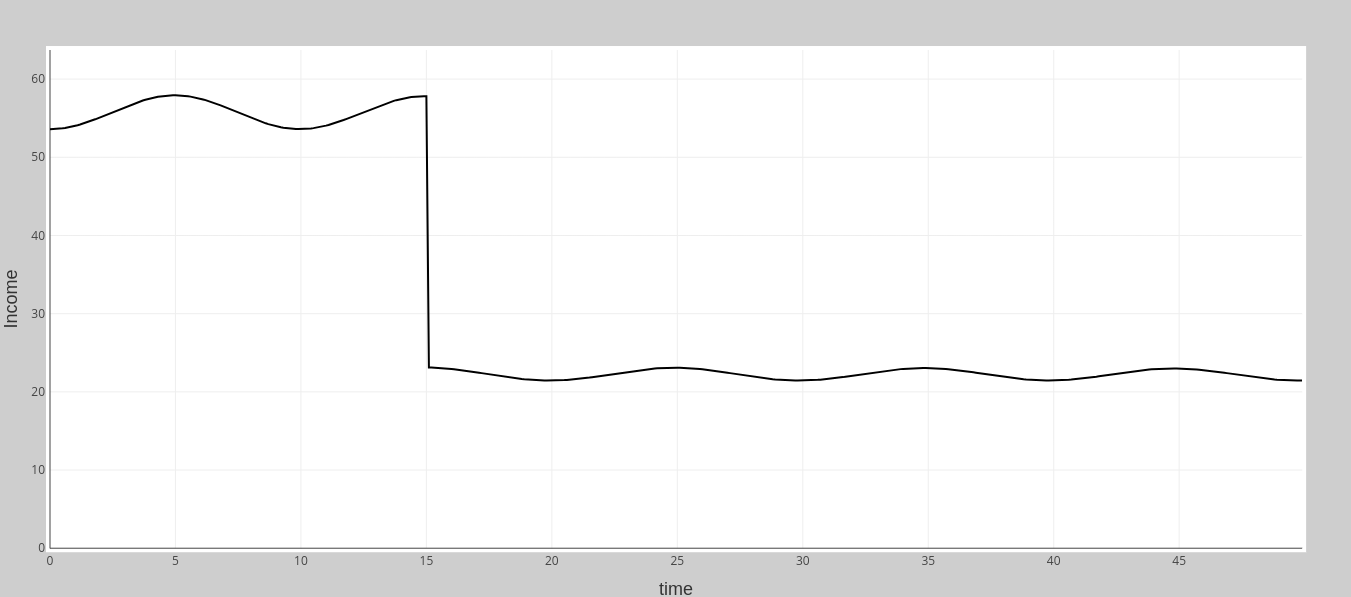
Nous pouvons illustrer dans cette application l’effet d’un changement de part des profits, basé sur les propres équations de l’Essay de Kalecki.
Kalecki exprime le profit en termes de la part de profit et de degré d’utilisation du stock de capital:
Nous posons que 
, c’est-à-dire que la part de profit est constante de sorte que 
. Cette équation pour 
détermine une droite dans le plan 
qui correspond aux profits potentiels que l’entreprise pourrait réaliser si elle parvenait à vendre toute sa production. Conformément à la théorie du profit de Kalecki, les profits réalisés par l’entreprise sont déterminés par les dépenses des capitalistes. Cela peut être vu si l’on exprime le revenu agrégé en termes de salaires et de profits d’un côté et de consommation et d’accumulation de l’autre côté de sorte que 
. Comme Kalecki suppose que tous les salaires sont consommés et que les capitalistes consomment une petite fraction de leurs profits (
), on obtient l’équation des profits ci-dessous.
En égalant les deux équations pour P, nous obtenons une équation pour Y en fonction de A:
Cela nous donne la dynamique du revenu national. Elle montre qu’après un choc sur c (changement de la part de profit), le revenu s’ajustera à un nouveau niveau (voir le panneau « Revenu » dans l’application ci-dessus), tandis que le taux de profit 
restera inchangé (panneau « Taux de profit »).
À la réunion de Leyde, Fisher exhorte ses collègues économètres à changer leur vision et à envisager la possibilité que l’économie ne soit stable que dans le voisinage de son état stationnaire (Fisher, 1933). À cette conjoncture particulière, alors que la crise paraît interminable, Tinbergen est le premier à remettre en question l’idée de stabilité. Il propose alors une nouvelle approche avec l’idée qu’il peut y avoir plusieurs équilibres dans l’économie, et que certains d’entre eux peuvent être instables et conduire à un effondrement partiel ou complet. Frisch, contre toute attente mais aussi en référence à Fisher, propose également d’intégrer cette idée dans ses propres modèles. Mais ce n’est pas le cas pour Kalecki qui « reste campé sur ses positions » pour reprendre les termes de Samuelson. \end{document}