Ce post se fonde sur des résultats exposés dans le chapitre 3 de Modeling Economic Instability: A History of Early Macroeconomics (33-53). Tous les commentaires sont les bienvenus.
Au tournant des années 1920-1930, les modèles économiques dynamiques formulés sous forme mathématique étaient encore rares. Des avancées sont réalisées à la suite de la découverte de nouvelles régularités économiques établies à partir de données statistiques récentes. L’économiste Carl Snyder (un des seize fondateurs de la Société d’Econométrie créée en 1930) découvre que l’amplitude des mouvements économiques est limitée sur longue période. Seule change la récurrence de ces mouvements, révélant que malgré tous les efforts de lissage des données, certains booms sont plus courts, certaines dépressions durent plus longtemps, de sorte qu’il existe une forte asymétrie entre les périodes d’expansion et de récession.
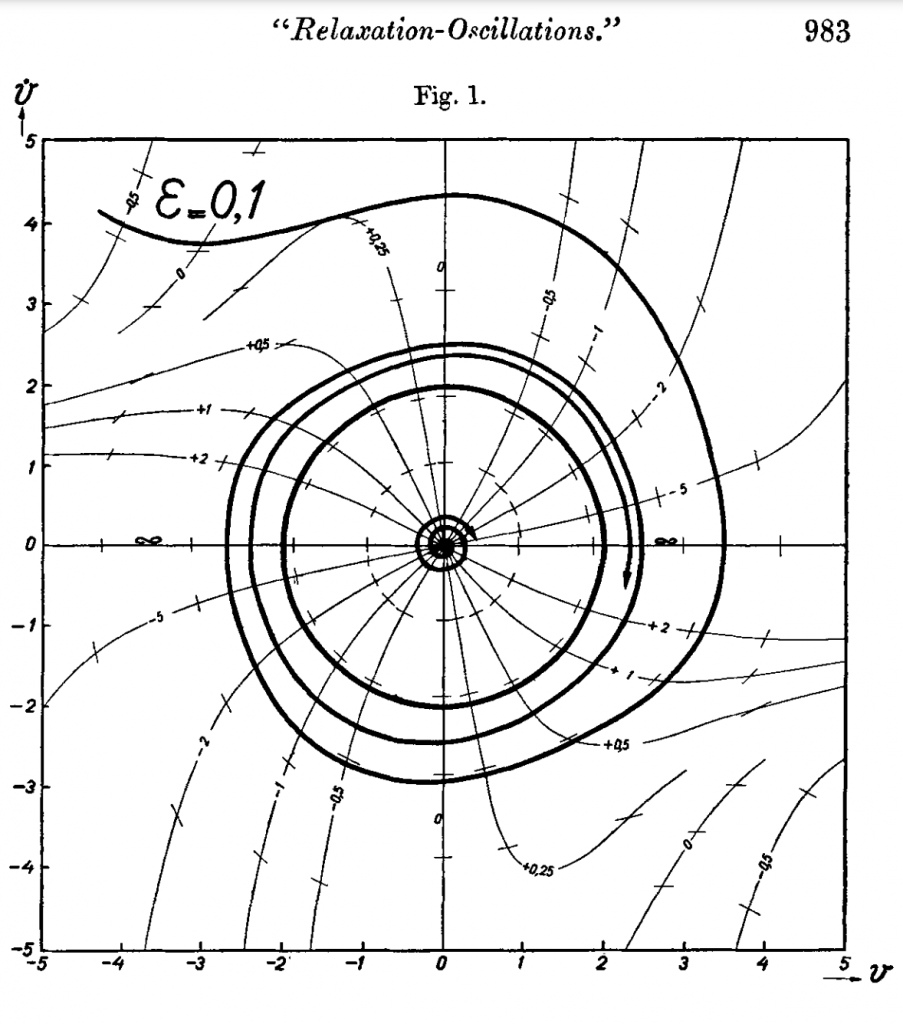
Pour capturer ces propriétés dans un modèle, l’ingénieur néerlandais Ludwig Hamburger, qui se penche sur la question des cycles économiques à la suite de la crise de 1929 (Hamburger, 1930 ; 1931), s’inspire du travail récent d’un autre Néerlandais, le physicien Balthasar van der Pol (1926 ; 1928 ; 1930), qui voit dans dans un nouveau type d’équation non linéaire la possibilité d’expliquer de nombreux phénomènes physiques, électriques et même mécaniques. Ce sont ces équations, que Van der Pol choisit de baptiser « équations de relaxation » et qu’Hamburger reprend presque mot pour mot dans sa présentation sur les cycles économiques.
Une des caractéristiques essentielle de ces équations est de posséder un coefficient de résistance (
) non linéaire, de sorte que toute perturbation de l’équilibre sera suivie temporairement par des oscillations explosives, avant stabilisation du système (cycle limite) :
Un autre mérite de cette équation est de montrer que les oscillations ne sont pas nécessairement sinusoïdales en raison de phénomènes soudains de « charge » ou de « décharge ». En effet, une fois que la variable endogène atteint un plafond ou un plancher, elle s’éloigne lentement de celui-ci, jusqu’à ce qu’un point de rupture soit atteint et qu’elle bascule alors vers une valeur élevée ou faible.
En cela, Hamburger pensait, comme von der Pol qui appliquait ses découvertes à des problèmes biologiques tels que le battement de cœur, que ces équations pouvaient être un moyen de sortir d’une vison trop mécanique représentée par les oscillations d’un pendule. En sortant de cette vision pendulaire, Hamburger voit une opportunité nouvelle d’analyser les effets des chocs sur un système et de montrer que si ces chocs ne modifient pas l’amplitude des oscillations, ils exercent en revanche un effet sur leur fréquence.
L’application suivante reproduit une simple oscillation de van der Pol basée sur l’équation ci-dessus, et permet à l’utilisateur d’ajouter un choc qui est normalement distribué avec une moyenne 
et un écart-type 
.
Les idées de Hamburger furent initialement bien accueillies parmi les premiers membres de la Société d’Econométrie. Ragnar Frisch, le fondateur et principal promoteur de la société, s’était intéressé (Frisch, 1928) au problème de la compréhension des séries chronologiques caractérisée par une périodicité changeante. Il félicita Hamburger, considérant que son explication mélangeant chocs et oscillations de relaxation était nettement supérieure à la sienne. Ce n’est donc pas un hasard si Hamburger fut invité aux premières réunions de la Société d’économétrie. Pourtant, cette approche ne fut pas retenue par les autres économètres et « macrodynamistes » pour au moins trois raisons.
En premier lieu, il convient de se rappeler que des progrès sont réalisés au même moment à partir de modèles économiques dynamiques qui donnaient un nouveau sens aux chocs et à la source des oscillations. Tinbergen (1933), Kalecki (1935) et Frisch (1933) parviennent en particulier à construire des modèles dérivés d’une analyse de mécanismes économiques, ce que Hamburger ne réussit à faire, ne dépassant pas le stade de l’analogie.
De surcroît, l’angle d’analyse des « macrodynamistes » se transforme à mesure que la dépression s’aggrave. Frisch et surtout Tinbergen construisent des modèles montrant la possibilité d’une instabilité globale, un effondrement de l’économie et non plus de cycles limites autour d’une position d’équilibre (deux autres posts sur ce blog décrivent l’approche de Tinbergen ici et ici).
Enfin, l’idée présentée par Frisch en 1933, selon laquelle les oscillations économiques étaient amorties et périodiquement maintenues par des impulsions externes, s’impose comme l’approche dominante des oscillations, éclipsant en même temps à l’approche endogène incarnée par Hamburger.
L’approche est finalement relancée vingt ans plus tard ; l’ironie du sort veut que c’est par l’intermédiaire de Philippe le Corbeiller, un ingénieur français qui avait également été invité à donner son point de vue sur les oscillations de relaxation au début des années 1930, que ces équations font leur retour dans la science économique à la fin des années 1940. À cette époque, le Corbeiller occupe un poste de physicien à l’Université d’Harvard, où il rencontre Richard Goodwin qu’il convainc de l’intérêt d’utiliser ces équations pour construire de nouveaux modèles macrodynamiques. En parvenant enfin à articuler cette équation à des mécanismes économiques clairs (accélérateur et multiplicateur), Goodwin ouvre définitivement la voie à une analyse non linéaire nouvelle des cycles.
Réferences:
Link vers notre WP: